Google Valentine Day Easter Egg: Algebraic Equation!

@thebigk • Oct 22, 2024

Oct 22, 2024

1.1K

If you want to impress your friends with your Google search abilities; enter the following search query in Google search bar and hit enter.

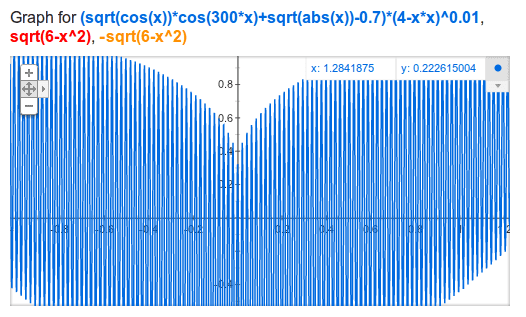
sqrt(cos(x))*cos(300x)+sqrt(abs(x))-0.7)*(4-x*x)^0.01, sqrt(6-x^2), -sqrt(6-x^2) from -4.5 to 4.5

☕ What gives?

Like 0 Replies 6

Replies

Welcome, guest

Join CrazyEngineers to reply, ask questions, and participate in conversations.

CrazyEngineers powered by Jatra Community Platform

Dancer_Engineer

@dancer-engineer-EJ8rGI • Feb 9, 2012

Valentine Day does not exist for year 2012!

Want proof?

Here: 14-02-12 = 0

😁
0

Anoop Kumar

@anoop-kumar-GDGRCn • Feb 9, 2012

This one looks better:
Copy n paste in google

 
sqrt(cos(x))*cos(180x)+sqrt(abs(x))-0.7)*(4-x*x)^0.01, sqrt(6-x^2), -sqrt(6-x^2) from -4 to 4

hit enter

Anoop Kumar

@anoop-kumar-GDGRCn • Feb 9, 2012
The_Big_K
If you want to impress your friends with your Google search abilities; enter the following search query in Google search bar and hit enter.
```
sqrt(cos(x))*cos(300x)+sqrt(abs(x))-0.7)*(4-x*x)^0.01, sqrt(6-x^2), -sqrt(6-x^2) from -4.5 to 4.5
```
☕ What gives?
There is warning in your code: The function might not be plotted correctly. 😛😁
0
Kaustubh Katdare

@thebigk • Feb 9, 2012

ianoop
There is warning in your code: The function might not be plotted correctly. 😛😁
Looks like you didn't copy the complete code (there's a horizontal scrollbar). Or maybe Google doesn't heart you? 😒

Kidding!
0
PraveenKumar Purushothaman

@praveenkumar-66Ze92 • Feb 9, 2012
ianoop
This one looks better:
Copy n paste in google
```
 
sqrt(cos(x))*cos(180x)+sqrt(abs(x))-0.7)*(4-x*x)^0.01, sqrt(6-x^2), -sqrt(6-x^2) from -4 to 4
 
```
hit enter
This is kinda corrugated! Biggie's one was the BEST! 😛
0
circularsquare

@circularsquare-CAswn0 • Feb 9, 2012

When I saw it at first I wracked my brains over how the plot is 'shaded'. Because by definition a function is such that for a particular value of x , there is only one value of y.

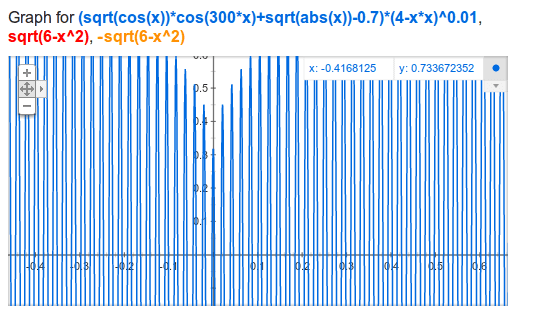
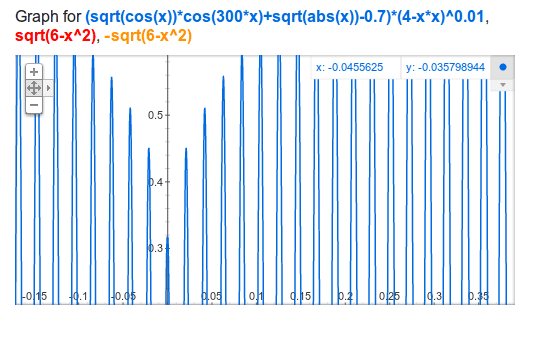
But I noticed that the image is a very zoomed out version of the plot. If you zoom in it has got closely spaced sine-like curve. The zoomed-out version of the plot & the closely-spaced zero crossings give an impression of 'shaded' region. So it is indeed a function with each value of x having at most one value of y.

Nice job.

0