Aruwin
Member • Nov 9, 2013
DFT and harmonic amplitude
Harmonic frequency = kf_r = αf_c + βf_r=α(20f_r) + βf_r = (20α+β)f_r.
Here, signal frequency f_r =f= ω_r/2π = 50Hz.
carrier frequency f_c = ω_c/2π=1kHz
Find the amplitude of the inverter's output waveform with frequency= 50Hz, of the following cases (when alpha, beta, and k are equals to those numbers in the table), and draw a bar graph using Excel. The DFT has been calculated and it's 3.030972661. The formula to finding the DFT is also given (See pic below).
The DFT gives two amplitude components for the cos and sin contribution, the total amplitude is the root of the sum of squares of both.
The frequency of the inverter's output wave is 50Hz.
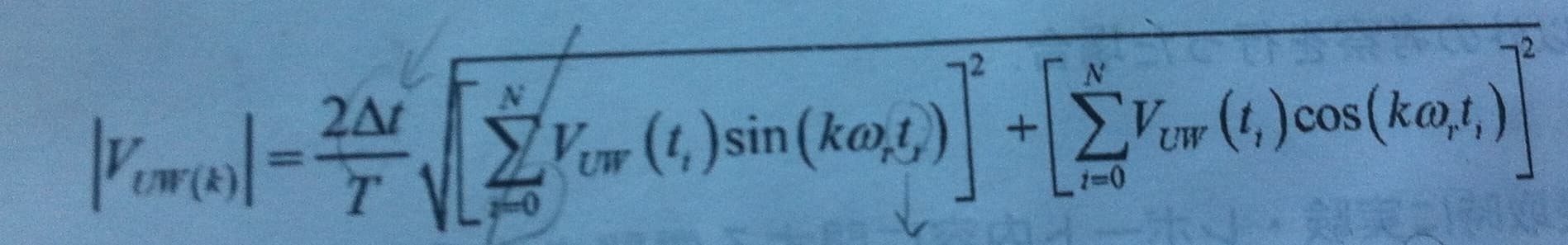
Here, signal frequency f_r =f= ω_r/2π = 50Hz.
carrier frequency f_c = ω_c/2π=1kHz
Find the amplitude of the inverter's output waveform with frequency= 50Hz, of the following cases (when alpha, beta, and k are equals to those numbers in the table), and draw a bar graph using Excel. The DFT has been calculated and it's 3.030972661. The formula to finding the DFT is also given (See pic below).
The DFT gives two amplitude components for the cos and sin contribution, the total amplitude is the root of the sum of squares of both.
The frequency of the inverter's output wave is 50Hz.
