Need help about charged ring
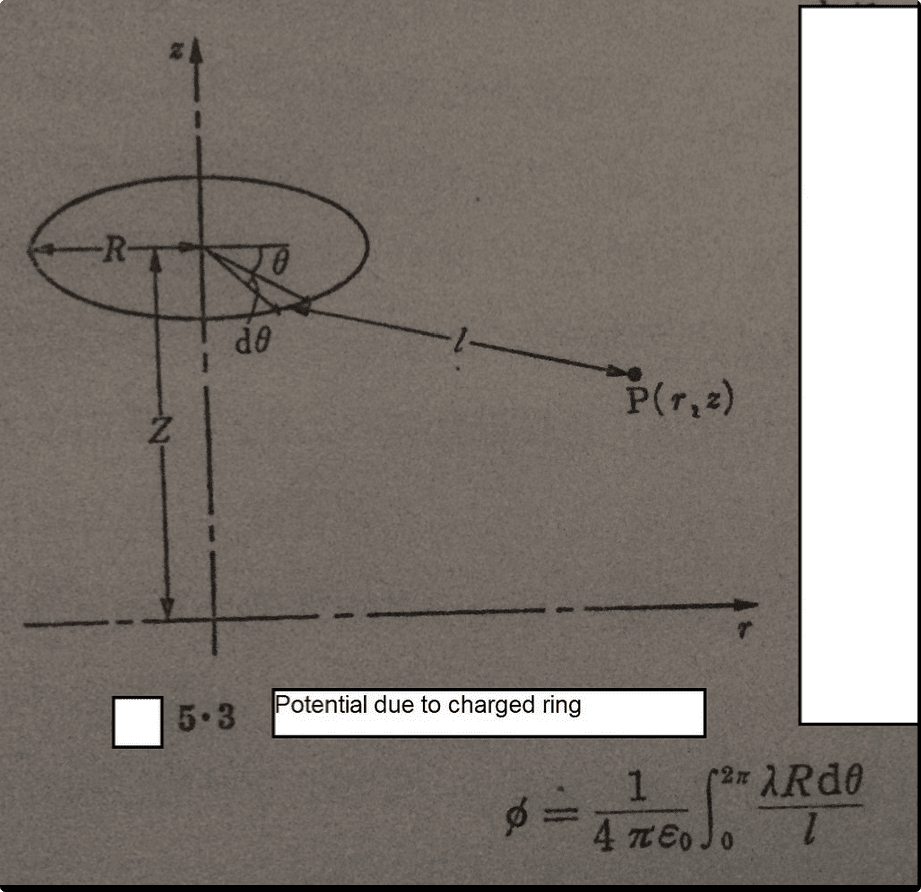
The picture above shows the potential due to ring charge. (you need to right click on the picture box and open on new tab)
Please show the full steps of deriving the equation of electrical potential above.
NOTE:
The electric potential of the revolving symmetrical ring electric charge related to the axis z as depicted in the diagram 5.3, is also called a charged coil or a charged ring in the electromagnetism books, but most of the time, it gives an infinite series of equation that uses Legendre function. It is commonplace to use complete circle integral function in the charge simulation method. If the position (height) of ring electric charge is Z, the radius is R, and the charge density is λ, the electric potential of the point P will be as represented in the next equation.
In the equation, l is the distance between the part of the ring charge dθ and P.
