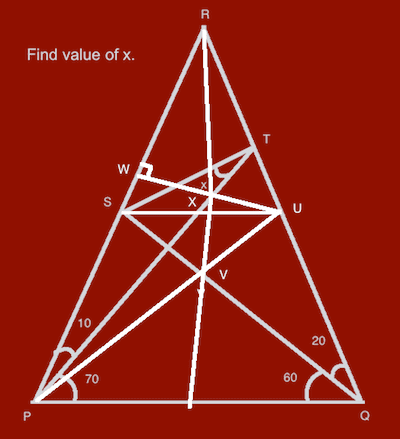
Solution to Grand Quiz Question #2

From figure we have,


[1] PR = QR
[2] QS = SR
-----------------------------------------------



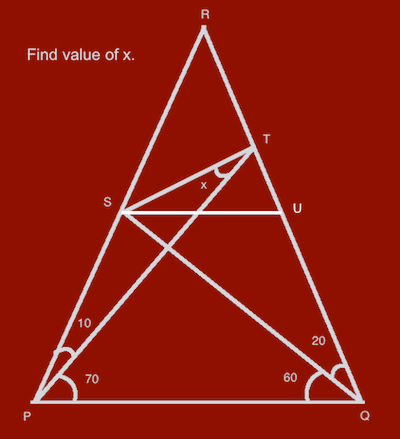
In Figure 2, parallel to PQ, we draw SU
Because [1] and PQ || SU, we get
[3] RS =RU
[4] PS = QU
-----------------------------------------------



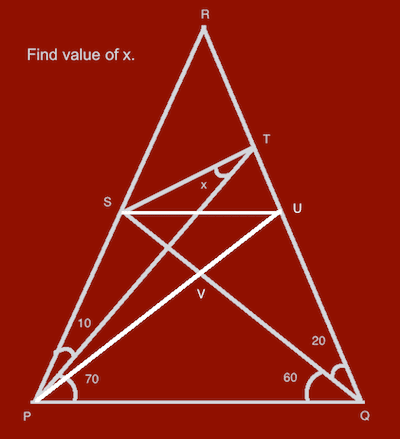
In Figure 3, we draw line PU.
From [4], and PQ = QP, and angle RPQ = RQP (=80),
the triangle PQS equals to triangle PQU.
So
[5] PU = QS
From [2], PU = SR
From [3], we get
[6] PU = RU
So angle RPU = 20, TPU = 10, UPQ = 60,
[7] SVU = 60
[8] PQ = QV = VP
From [5], [7] and [8], we get
[9] SU = UV = VS
-----------------------------------------------



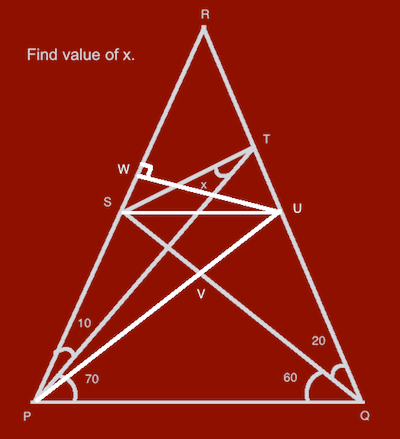
In Figure 4, we draw UW vertical to PR.
From [6] and angle RPU = PRU, we get triangle PUW equals to triangle RUW. So
[10] PW = RW
-----------------------------------------------



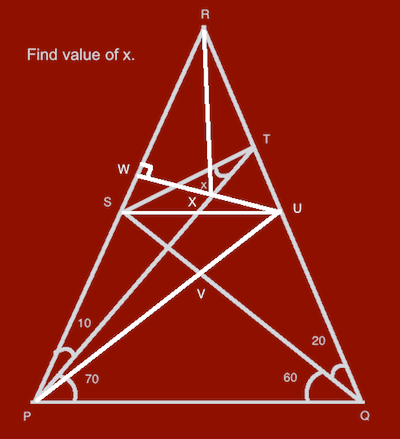
Figure 5
In Figure 5, we draw RX.
From [10] and UW vertical to PR, we get
[11] angle SRX = SPX = 10
[12] RX = PX
From [11], we get
[13] angle URX = 10 = SRX
[13'] angle URX = UPX