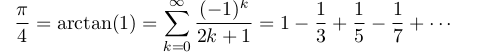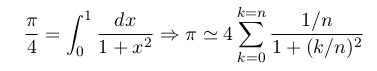Abhishek Rawal
@#-Link-Snipped-# No hurry,buddy. Good luck for your project 😀
In my assignment, I had to compare the execution time of programs implemented :
1- without OpenMP
2 - using OpenMP
I only used Icc because it was required. (I could have done the same thing using gcc)
(To get sarted on openMP #-Link-Snipped-#)
1 - the mandelbrot fracatal:
(I you want to get an idea about what it is you can go to http <a href="https://en.wikipedia.org/wiki/Mandelbrot_set" target="_blank" rel="nofollow noopener noreferrer">Mandelbrot Set</a>)
int mandelbrot (float a, float b, int max_iter)
{
int iter = 0;
float x=0, y=0;
while(( iter < max_iter ) && ( x*x + y*y <= 4.0) )
{
x = x*x - y*y + a;
y = 2*x*y + b;
iter++;
}
return iter;
}
Now, that's a simple program, but one has to be careful when adding the openmp pragma because a segmentation fault can easily araise (and that's what happened to me)
int mandelbrot (float a, float b, int max_iter)
{
int iter = 0;
float x=0, y=0;
[B]omp_set_num_threads([number of threads]); [/B]
[B]#pragma omp parallel for private(iter,a,b) schedule([scheduling type], [chunksize ])[/B]
while(( iter < max_iter ) && ( x*x + y*y <= 4.0) )
{
x = x*x - y*y + a;
y = 2*x*y + b;
iter++;
}
return iter;
}
I compared the execution times when choosing static and dynamic scheduling (in both scheduling patterns I gave the threads the same number of iterations to process).
The result is : the bigger the numbre of threads id, the faster the program is executed. I'm not sur whether it's correct or not, but it seems to me logical. I read somewhere that depending on the number of cores of the computer, there's an optimal combination of the number of threads, the scheduling policy and the chunk size.
I have a dual core machine, and the optimal combination in my case was:
number of threads = 8
scheduling policy = dynamic
chunk size = max_iter/number of threads
so in more concrete words :
for max_iter = 256 (to have 256 levels of gray), I wrote:
[....]
omp_set_num_threads(8);
#pragma omp parallel for private(iter,a,b) schedule(dynamic, 64)
[....]
I didn't try for more than 8 threads, but maybe I could have had a faster program if I had tried it.
As for the best scheduling policy, in this case it's dynamic scheduling. Logical, because the amount of work that each iteration contains depends on the value of the exiting iteration.
I have though some questions on which I've been ruminating, since I got these results:
-Why would a lower number of threads give better results?
-When I didn't use the private(iter,a,b) clause I kept getting a segmentation fault, bur why?
2-Calculation of pi
We have
There are 2 formulas to implement
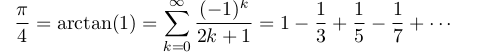
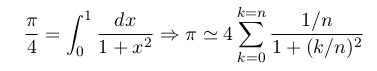
The second one gave better results in terms of precision and time of execution, BUT:
I couldn't implement the OpenMP at all! I kept getting the segmentation fault no matter how I tried!
here's my program:
double integrale(int64 n)
{
double pi = 0.0;
int i; double x,sum; int id;
double step = 1.0/(double)n;
omp_set_num_threads(2);
#pragma omp parallel private(x,sum)
{
id = omp_get_thread_num();
for(i=id,sum=0.0;i<n;i=i+2)
{
x = ((double)i-0.5)*step;
sum += 4.0/(1.0+x*x);
}
#pragma omp critical
pi += sum*step;
}
retrun pi;
}
What could be that created the problem?